Активные фильтры
Электрическим фильтром называется устройство для передачи электрических сигналов, пропускающее токи в определенной области частот и препятствующее их прохождению вне этой области. В радиотехнике и электронике электрические фильтры подразделяют на пассивные и активные. Схемы пассивных фильтров содержат только пассивные элементы: резисторы, конденсаторы и катушки индуктивности.
В схемы активных фильтров помимо указанных элементов входят такие активные изделия, как транзисторы или интегральные микросхемы. Фильтрующие свойства устройства определяются его амплитудно-частотной характеристикой, которой называется зависимость коэффициента усиления этого устройства от частоты сигнала. В некоторой области частот, которая называется полосой пропускания или полосой прозрачности, электрические колебания передаются фильтром с входа на выход практически без ослабления. Вне полосы прозрачности расположена полоса затухания или задерживания, в пределах которой частотные составляющие сигнала ослабляются. Между полосой прозрачности и полосой задерживания находится частота, называемая граничной. В связи с тем что существует плавный переход между полосой прозрачности и полосой затухания, граничной обычно считается частота, на которой ослабление сигнала оказывается равным -3 дБ - то есть по напряжению в √2 раз меньше, чем в полосе прозрачности.
Всегда интересно получить крутой переход амплитудно-частотной характеристики между полосой прозрачности и полосой затухания. В пассивных фильтрах увеличения крутизны такого перехода добиваются усложнением схемы и применением многозвенных систем. Сложные фильтры требуют громоздких расчетов и точной настройки. Активные фильтры благодаря использованию обратной связи оказываются значительно проще и дешевле.
Принято подразделять фильтры на четыре категории в зависимости от расположения полосы прозрачности:
• фильтры нижних частот (0 ≤ f ≤ f0);
• фильтры верхних частот (f ≥ f0);
• полосовые фильтры (f01 ≤ f ≤ f02);
• заграждающие или режекторные фильтры (0 ≤ f ≤ f01 и f ≥ f02).
Здесь f - частота сигналов, проходящих через фильтр; f0 -граничная частота; f01 - нижняя граничная частота; f02 - верхняя граничная частота. Таким образом, фильтр нижних частот nponycкает составляющие сигнала, частота которых меньше граничной частоты; фильтр верхних частот пропускает составляющие сигнала, частота которых больше граничной частоты; полосовой фильтр пропускает составляющие сигнала, частота которых находится между нижней граничной частотой f01 и верхней граничной частотой f02; наконец режекторный фильтр ослабляет сигналы, частота которых находится между нижней граничной f01 и верхней граничной f02 частотами. Существуют и более сложные фильтры специального назначения, например гребенчатый фильтр, применяемый в цветном телевидении, пропускающий много узких полос и ослабляющий промежутки между ними.
Электрические фильтры находят широкое применение в электротехнике, радиотехнике и электронике. Так на выходе выпрямителей используется фильтр нижних частот, пропускающий только постоянную составляющую выпрямленного тока и ослабляющий прохождение пульсаций. В радиоприемниках широко используются полосовые фильтры, которые позволяют выделить из принятых антенной сигналов множества радиостанций только один, полоса частот которого оказывается в полосе прозрачности фильтра.
Принято еще одно деление всех фильтров на две категории: фильтры, схема которых содержит катушки индуктивности, и фильтры без индуктивностей, RC-фильтры или резисторно-конденсаторные фильтры.
Активные резисторно-конденсаторные фильтры имеют огромное преимущество перед их пассивными аналогами, особенно на частотах ниже 10 кГц. Пассивные фильтры для низких частот должны содержать катушки большой индуктивности и конденсаторы большой емкости. Поэтому они получаются громоздкими, дорогостоящими, а их характеристики оказываются далеко не идеальными.
Большая индуктивность достигается за счет большого числа витков катушки и применения ферромагнитного сердечника. Это лишает ее свойств чистой индуктивности, так как длинный провод многовитковой катушки обладает заметным сопротивлением, а ферромагнитный сердечник подвержен влиянию температуры на его магнитные свойства. Необходимость же использования большой емкости вынуждает применять конденсаторы, обладающие плохой стабильностью, например электролитические. Активные фильтры в значительной мере лишены указанных недостатков.
Схемы дифференциатора и интегратора, построенные с применением операционных усилителей, представляют собой простейшие активные фильтры. При выборе элементов схемы в определенной зависимости от частоты дифференциатор становится фильтром верхних частот, а интегратор - фильтром нижних частот. Далее будут рассмотрены примеры других более сложных и наиболее универсальных фильтров. Большое количество других возможных схем активных фильтров вместе с их детальным математическим анализом можно найти в разных учебниках и пособиях.
Фильтры нижних частот
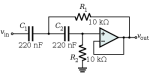
Если объединить схему инвертирующего усилителя со схемой интегратора, образуется схема фильтра нижних частот первого порядка, которая показана на рис. 1.
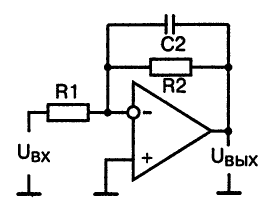
Рис. 1. Схема активного фильтра нижних частот первого порядка
Такой фильтр представляет собой инвертирующий усилитель, обладающий постоянным коэффициентом усиления в полосе прозрачности от постоянного тока до граничной частоты f0. Видно, что в пределах полосы прозрачности, пока емкостное сопротивление конденсатора достаточно велико, коэффициент усиления схемы совпадает с коэффициентом усиления инвертирующего усилителя:
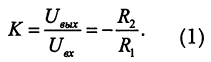
Граничная частота этого фильтра определяется элементами цепи обратной связи в соответствии с выражением:
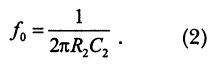
Амплитудно-частотная характеристика - зависимость амплитуды сигнала на выходе устройства от частоты при постоянной амплитуде на входе этого устройства - представлена на рис.2.
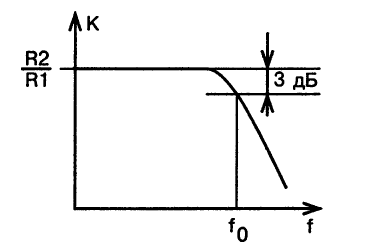
Рис. 2. Амплитудно-частотная характеристика фильтра нижних частот первого порядка
В полосе затухания выше граничной частоты f0 усиление уменьшается с интенсивностью 20 дБ/декада (или 6 дБ/октава), что означает уменьшение коэффициента усиления по напряжению в 10 раз при увеличении частоты также в 10 раз или уменьшение коэффициента усиления в два раза при каждом удвоении частоты.
Если такой крутизны наклона амплитудно-частотной характеристики в полосе затухания недостаточно, можно использовать фильтр нижних частот второго порядка, схема которого показана на рис.З.
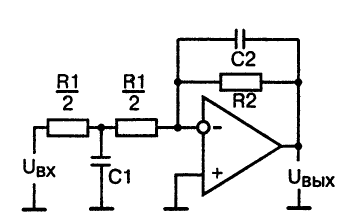
Рис. З. Принципиальная схема активного фильтра нижних частот второго порядка
Коэффициент усиления фильтра нижних частот второго порядка такой же, как у фильтра первого порядка, в связи с тем что суммарное сопротивление резисторов в цепи инверсного входа, как и ранее, выражается значением R1:
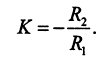
Граничная частота при выполнении условия R1C1 = 4R2C2 также выражается прежней формулой:
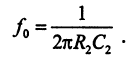
Что касается амплитудно-частотной характеристики этого фильтра, представленной на рис. 4, то она отличается повышенной крутизной наклона, которая составляет 12 дБ/октава.
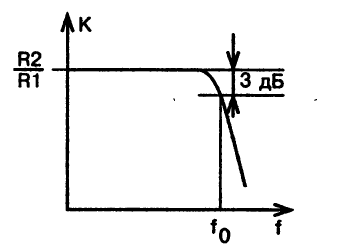
Рис. 4. Амплитудно-частотная характеристика фильтра нижних частот второго порядка
Таким образом, в полосе затухания при увеличении частоты вдвое напряжение сигнала на выходе фильтра уменьшается в четыре раза.
Фильтры верхних частот
Аналогично построена схема фильтра верхних частот, которая представлена на рис.5. Такой фильтр является инвертирующим усилителем с постоянным коэффициентом усиления в полосе прозрачности от частоты f0 и более. В полосе прозрачности коэффициент усиления схемы такой же, как у инвертирующего усилителя:
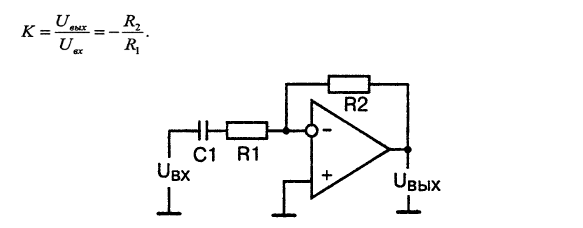
Рис.5. Принципиальная схема активного фильтра верхних частот первого порядка
Граничная частота f0 на уровне -3 дБ задается входной цепью в соответствии с выражением:
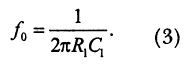
Крутизна наклона амплитудно-частотной характеристики, которая представлена на рис.6, в области граничной частоты составляет 6 дБ/октава.
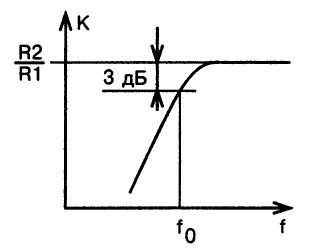
Рис.6. Амплитудно-частотная характеристика фильтра верхних частот первого порядка
Как и в случае фильтров нижних частот, можно собрать активный фильтр верхних частот второго порядка в целях повышенного подавления сигнала в полосе затухания. Принципиальная схема такого фильтра показана на рис.7.
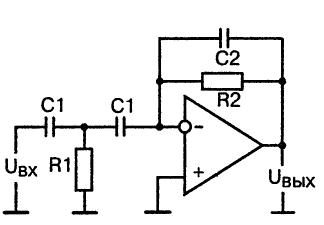
Рис.7. Принципиальная схема активного фильтра верхних частот второго порядка
Крутизна наклона амплитудно-частотной характеристики фильтра верхних частот второго порядка в области граничной частоты составляет 12 дБ/октава, а сама характеристика показана на рис.8.
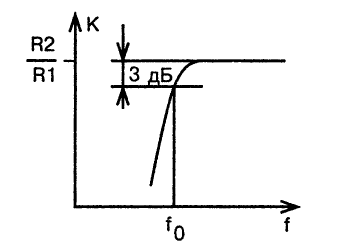
Рис.8. Амплитудно-частотная характеристика фильтра верхних частот второго порядка
Полосовые фильтры
Если объединить активный фильтр нижних частот с активным фильтром верхних частот, то в результате образуется полосовой фильтр, принципиальная схема которого приведена на рис.9.
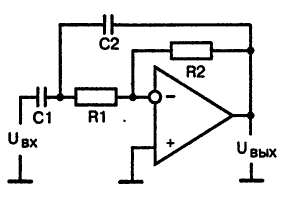
Рис. 9. Принципиальная схема активного полосового фильтра
Эту схему иногда называют избирательным усилителем с ин-тегродифференцирующей обратной связью. Подобно усилителям, содержащим колебательные контуры, полосовой фильтр также имеет амплитудно-частотную характеристику с выраженным максимумом на определенной частоте. Называть такую частоту резонансной нельзя, так как резонанс возможен только в контурах, образованных индуктивностью и емкостью. В других случаях частоту такого максимума обычно называют частотой квазирезонанса. Для рассматриваемого полосового фильтра частота квазирезонанса f0 определяется элементами цепи обратной связи:
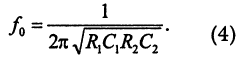
Амплитудно-частотная характеристика этого полосового фильтра показана на рис. 10.
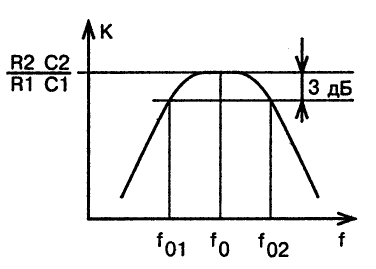
Рис.10. Амплитудно-частотная характеристика полосового фильтра
Максимальный коэффициент усиления на частоте квазирезонанса оказывается равным:
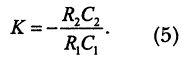
Относительная полоса пропускания на уровне -3 дБ:
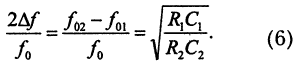
Принципиальная схема еще одного полосового фильтра приведена на рис. 11.
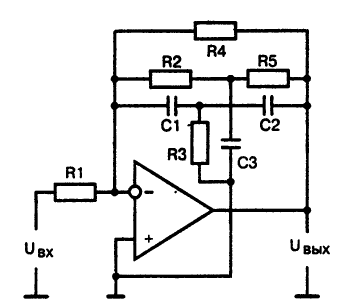
Рис. 11. Принципиальная схема полосового фильтра с двойным Т-фильтром
Здесь в цепь отрицательной обратной связи включен двойной Т-фильтр, образованный резисторами R2, R3, R5 и конденсаторами Cl, С2, СЗ.
Как известно, если выполняются следующие условия: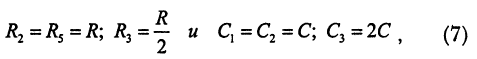
амплитудно-частотная характеристика двойного Т-фильтра содержит квазирезонанс, частота которого равна
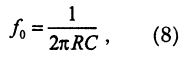
причем на частоте квазирезонанса коэффициент передачи двойного Т-фильтра равен нулю. Поэтому активный фильтр с двойным Т-фильтром, включенным в цепь отрицательной обратной связи, является полосовым фильтром с максимумом амплитудно-частотной характеристики на частоте квазирезонанса. Три такие характеристики представлены на рис. 12. Характеристики различаются разными сопротивлениями резистора R4: нижняя соответствует R4 = 100 кОм, средняя - R4 = 1 МОм, верхняя - R4 = ∞.
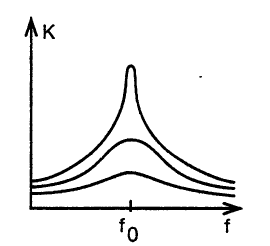
Рис. 12. Амплитудно-частотная характеристика активного фильтра с двойным Т-фильтром в цепи отрицательной обратной связи
Режекторные фильтры
Тот же самый двойной Т-фильтр может быть включен не в цепь отрицательной обратной связи, как это сделано при создании полосового фильтра, а в цепь входного сигнала. При этом образуется активный режекторный фильтр, схема которого приведена на рис, 13.
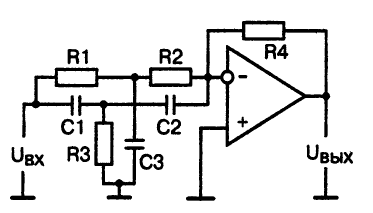
Рис.13. Принципиальная схема режекторного фильтра с двойным Т-фильтром
При выполнении прежних условий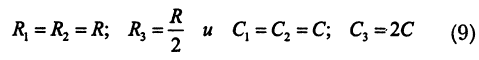
амплитудно-частотная характеристика активного фильтра, имеющего во входной цепи двойной Т-фильтр, содержит квазирезонанс, частота которого по-прежнему определяется фор мулой (8). Но на частоте квазирезонанса коэффициент усиления этого активного фильтра равен нулю. Амплитудно-частотная характеристика активного фильтра с двойным Т-фильтром во входной цепи показана на рис.14.
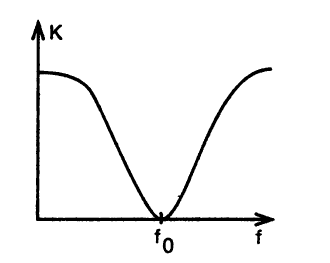
Рис. 14. Амплитудно-частотная характеристика активного фильтра с двойным Т-фильтром во входной цепи
Сложные фильтры
Несколько активных фильтров можно соединять последовательно для получения амплитудно-частотной характеристики с повышенной крутизной наклона. Кроме того, соединенные последовательно секции простых фильтров имеют пониженную чувствительность. Это означает, что небольшое отклонение величины одного из компонентов схемы (отклонение сопротивления резистора или емкости конденсатора от нормы) будет приводить к меньшему влиянию на окончательную характеристику фильтра, чем в случае аналогичного сложного фильтра, построенного на одном операционном усилителе.
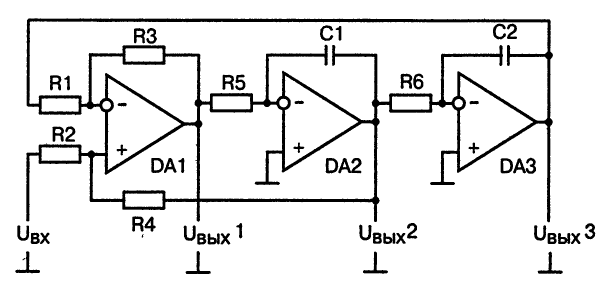
Рис. 15. Принципиальная схема ступенчатого фильтра
На рис. 15 показан ступенчатый фильтр, собранный из трех операционных усилителей. Популярность таких фильтров резко возросла после появления в продаже интегральных микросхем, содержащих несколько операционных усилителей в одном корпусе. Достоинствами этого фильтра являются низкая чувствительность к отклонениям величин компонентов и возможность получения трех выходов: верхних частот Uвых1, полосового Uвых2 и нижних частот UвыхЗ.
Фильтр составлен из суммирующего усилителя DA1 и двух интеграторов DA2, DA3, которые соединены в виде замкнутой петли. Если элементы схемы выбраны согласно условию![]()
то граничная частота оказывается равной
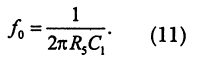
Выходы верхних и нижних частот имеют крутизну наклона амплитудно-частотной характеристики, равную 12 дБ/октава, а полосовой выход имеет треугольную характеристику с максимумом на частоте f0 с добротностью Q, которая определяется резисторами установки усиления микросхемы DA1.









