Система ФАПЧ и ее применения (Часть 2)

Частотные свойства системы ФАПЧ

    Передаточная функция (3) является функцией 1-го порядка. Применение фильтра в цепи ФАПЧ изменяет динамические свойства системы. Полином системы (многочлен в знаменателе передаточных функций) определяет порядок, вид аппроксимации и частотный диапазон фильтрации, а член или многочлен в числителе определяет вид фильтрации (нижних, верхних частот или полосовой фильтрации) и коэффициент передачи.

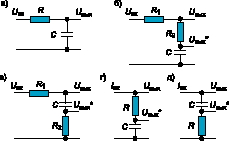
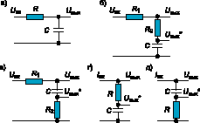
Рис. 6

    В системах ФАПЧ 2-го порядка обычно используется один из фильтров 1-го порядка, показанных на рис. 6 (отметим, что общепринятое название "фильтр" в данном случае является условным; правильнее было бы считать их цепями частотной коррекции):

• интегрирующий фильтр (ИФ) (рис. 6а) с передаточной функцией K_Ф(p) = U_вых/U_вх = 1/(1+pt_Ф) = k_Ф(p) при K_Ф = 1, где t_Ф = RC постоянная времени фильтра;
• пропорционально-интегрирующие фильтры (ПИФ) (рис. 6б,в) с передаточной функцией K_Ф(p) = U_вых/U_вх = = (1 + pt_Ф1)/(1 + pt_Ф) = k_Ф(p) при K_Ф = 1, где t_Ф = RC, t_Ф1 = R2C, R = R1 + R2;
• пропорционально-интегрирующие цепи (ПИ) (рис. 6г,д) с передаточной функцией K_Ф(p) = U_вых/I_вх = K_Фk_Ф(p), где K_Ф = R, k_Ф(p) = 1 + 1/pt_Ф1, t_Ф1 = RC.

    Цепь ПИ отличается от ИФ и ПИФ тем, что источником ее входного сигнала является источник тока I_вх с бесконечно большим сопротивлением. В системе ФАПЧ цепь ПИ реализуется, например, при помощи операционного усилителя с ПИ в качестве цепи параллельной отрицательной обратной связи. Передаточная функция цепи с усилителем равна K_Ф(p) = -(K_Ф + 1/pt_Ф) = -K_Фk_Ф(p), где K_Ф = R/r, t_Ф = rC, r токозадающее сопротивление цепи, включенное на входе усилителя, а k_Ф(p) согласно ПИ на рис. 6г,д. Знак минус, определяемый инвертирующим включением усилителя, должен учитываться в фазировке ФД, если ФД с пилообразной характеристикой. Отметим, что tФ является "физической" постоянной времени цепи ПИ, а также ПИФ, в то время как t_Ф1 условной постоянной времени, удобной для записи математических выражений. Передаточная функция ПИ, определяемая K_Ф + 1/pt_Ф, в отличие от ПИФ состоит из двух функций пропорциональной KФ и интегрирующей 1/pt_Ф. K_Ф влияет на добротность и, соответственно, на устойчивость системы (при KФ --> 0 система ФАПЧ неустойчива), а член 1/pt_Ф определяет интегрирующее свойство ПИ, обеспечивающее астатизм системы ФАПЧ по отношению к фазе. В последнее время вместо операционного усилителя, обеспечивающего токовую "запитку" ПИ, применяется токовый формирователь, используемый вместе с рассмотренным выше ЧФД. Указанный формирователь обеспечивает подключение ПИ "нижним" выводом к "земле". Отметим, что, наряду с простейшей RC-цепью на рис. 6г, в качестве ПИ используются цепи сложной конфигурации и, соответственно, более высоких порядков [4,10].

    Помимо основных выходов фильтров U_вых, подключаемых в системе ФАПЧ к входу УГ, на рис. 6б-д показаны дополнительные выходы U_вых*, которые, наряду с основными, могут быть использованы для съема выходного сигнала системы ФАПЧ [11]. Использование дополнительных выходов эквивалентно подключению внешних фильтров на выходе системы, не задействуемых в замкнутой петле обратной связи. Передаточные функции фильтров для дополнительных выходов, наряду с функциями для основных выходов, приведены в таблице.

    Полином передаточных функций системы ФАПЧ 2-го порядка, как и полиномиальных фильтров того же порядка, определяется обобщенным выражением 1 + p/w₀Q + p²/w₀², где w₀ собственная частота системы, известная в теории фильтров как частота полюсов, а Q добротность, определяющая вид аппроксимации частотных характеристик (по Баттерворту, Чебышеву и т.д.) [7]. В таблице приведены полиномы функций системы ФАПЧ с разными фильтрами, а также соответствующие им выражения Q и w₀. В таблице приведены также данные основной функции K_Dj(p) (4) и передаточной функции системы при ее использовании в качестве частотного демодулятора: K_ЧД^(p) с выходом после ФД (до фильтра), K_ЧД(p) после фильтра и KЧД*(p) при съеме сигнала с дополнительного вывода фильтра. Подчеркнем, что оператор p в передаточных функциях системы ФАПЧ определяется выражением jW, где W частота изменения частоты на входе и, соответственно, выходного напряжения (при частотной модуляции это частота модуляции).

    Анализируя данные, приведенные в таблице, можно сделать следующие выводы. Функция K_Dj(p) системы ФАПЧ 1-го порядка является функцией ФНЧ, а с ПИ функцией ПФ (полосовой фильтрации) с резонансной частотой w₀. Функция ПФ системы с ПИ определяет астатизм системы по отношению к фазе: коэффициент передачи на нулевой частоте равен нулю. Передаточная функция K_Dj(p) системы с ИФ и ПИФ является суммарной функцией ФНЧ и ПФ, которую можно рассматривать как функцию ФНЧ, измененную в области частоты среза. Напомним, что фильтрация 2-го порядка является фильтрацией нижних частот, если в числителе функции член нулевого порядка (t₀), и полосовой фильтрации, если первого порядка (pt₀t_Ф1).

    Функции K_ЧД(p) и K_ЧД*(p) для системы с ПИФ идентичны функциям для системы с ПИ, но они достигаются при указанных выше разных K_Dj(p). Применение дополнительных выходов, характеризуемых K_ЧД*(p), обеспечивает, в отличие от K_ЧД(p), получение передаточных функций типа ФНЧ (рис. 6б,г) и ПФ (рис. 6в,д), причем K_ЧД*(p) типа ФНЧ аналогична KЧД(p) системы с ИФ. Особенностью применения ПИФ, по сравнению с ИФ, является то, что требуемая добротность может быть задана изменением соотношения R2/R (t_Ф1/t₀) без изменения t₀ и t_Ф и, соответственно, без изменения w₀.

Применение системы ФАПЧ

    Применение системы ФАПЧ связано с тем, какой из ее элементов является входным, а какой выходным. Рассмотрим основные применения системы ФАПЧ.

    Частотный демодулятор. При использовании системы ФАПЧ в качестве частотного демодулятора ЧМ-сигнал подается на вход ФД (рис. 1а,в), а демодулированный снимается, например, с выхода фильтра. Передаточная функция демодулятора будет определяться выражениями числителя и знаменателя, приведенными в таблице, а также выражением (2). Для фильтрации демодулированного сигнала с требуемыми параметрами обычно используется дополнительный внешний фильтр. При этом систему ФАПЧ следует рассматривать как первую ступень фильтрации и соответствующим образом учитывать при расчете общей передаточной функции фильтра (с требуемыми порядком, аппроксимацией и частотой среза).

    Частотный модулятор. При использовании системы ФАПЧ в качестве частотного модулятора модулирующий сигнал uвх(t) подается на вход УГ, как показано на рис. 1б, а модулированный снимается с выхода УГ. При этом собственно модулятором является УГ, а система ФАПЧ задает несущую частоту, определяемую опорной (управляющей) частотой на входе ФД. Кроме того, в системе обеспечивается фильтрация модулируемого сигнала, определяемая выбранными параметрами передаточной функции. В общем виде, передаточная функция системы ФАПЧ в режиме ЧМ, в отличие от (2) для демодуляции,

К_ЧМ(р) = Dw_вых/u_вх = [pK₀/k_ф(р)/[1 + pt₀/k_ф(р)],

    где K₀ = t₀K_УГ. При использовании ПИФ

К_ЧМ(р) = (рК₀ + р²К₀t_ф)/(1 + pt₀ + p²t₀t_ф);     (9)

К_ЧМ*(р) = рК₀/(1 + pt₀ + p²t₀t_ф),     (10)

     соответственно для съема сигнала ЧМ с основного и дополнительного выходов ПИФ (рис. 6б). Функция (9) является суммарной функцией ПФ и ФВЧ, а функция (10) функцией ПФ. Второй вариант съема сигнала является более предпочтительным для узкополосных модулированных сигналов.

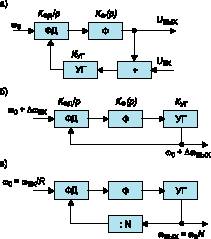
Рис. 7

    Частотные фильтры. На рис. 7а показана схема системы ФАПЧ с частотной фильтрацией напряжения uвх, а на рис. 7б с частотной фильтрацией модулирующего изменения частоты Dwвх в составе ЧМ-сигнала. Оба фильтра имеют одну и ту же передаточную функцию

К_ф(р) = 1/[1 + pt₀/k_ф(р)],

    являющуюся функцией ФНЧ при использовании ИФ и суммарной функцией ФНЧ и ПФ при использовании ПИФ и ПИ. Кроме того, первый из фильтров (рис. 7а) может быть использован со съемом сигнала с дополнительных выходов ПИФ и ПИ, для которых соответственно реализуются функции ФНЧ и ПФ.

    Фазовращатель. Выше показана зависимость постоянной разности фаз на входе ФД от режима работы системы ФАПЧ (рис. 5а,б). В соответствии с этим, при съеме сигнала с выхода УГ, как показано на рис. 7б, возможно получение фазового сдвига выходного сигнала, например, j₀ = p/2 или -p/2 (квадратурный фазовый сдвиг). Угол j₀ = p/2 обеспечивается при выборе характеристики ФД на рис. 2г, а j0 = -p/2 при "переполюсовке", например, источников E и -E. Возможны и другие значения углов.

    Умножитель частоты. Умножение частоты системой ФАПЧ обеспечивается при включении делителя частоты ":N" в цепь обратной связи, как показано на рис. 7в. Частота на выходе УГ, являющегося выходом умножителя, равна w_вых = w₀N, где N коэффициент деления делителя. В синтезаторах частот, на входе системы ФАПЧ дополнительно включают делитель частоты ":R" (на рис. 7в не показан). В результате, w₀ = w_вх/R, а w_вых = w_вхN/R, где R коэффициент деления делителя ":R". Совместное применение делителей ":R" и ":N" (с программируемыми коэффициентами деления) обеспечивает синтез частот в широком диапазоне и с высоким разрешением [4,10].

    Существенным для умножителей частоты является то, что пульсации на входе УГ могут иметь частоту wZ₀ или 2w₀ (в зависимости от типа ФД), которая значительно меньше частоты УГ, равной w₀N. В результате, это может привести к паразитной угловой модуляции сигнала УГ, проявляющейся в виде так называемого фазового шума. Для умножителей частоты, для которых характерен режим без модуляции, возможно применение низкочастотных фильтров, подавляющих указанные пульсации. Однако для синтезаторов частот, используемых в приемных и передающих каналах радиосвязи, где требуется достаточно быстрое переключение частоты, существенным является их быстродействие. Поэтому другой путь, широко реализуемый в настоящее время, это применение ЧФД (рис. 2д) с нулевым сигналом на его выходе (при использовании системы ФАПЧ в астатическом режиме) и относительно высокочастотного фильтра.

    Введение делителя частоты в цепь обратной связи повышает инерционность системы ФАПЧ: t₀ = N/K_ФДK_ФK_УГ. Инерционность может быть снижена введением дополнительного усиления, которое будет компенсировать влияние N, но есть другой путь. В синтезаторах частот используются, как указано выше, делители частоты типа "Integer-N" или "Fractional-N". Для последнего, в отличие от первого, характерны дробные числа коэффициента N. Поэтому значения N для "Fractional-N" могут быть меньшими (например, N = 10,25 вместо 1025 для "Integer-N") при соответственно большей (в те же 100 раз) величине w₀. При меньшей величине N будет меньшее влияние на t₀, а при соответственно большей величине w₀ облегчаются условия фильтрации сигнала ФД, поступающего на вход УГ.

    Умножение частоты может быть также реализовано в системе ФАПЧ с DDS-синтезатором в качестве де-лителя частоты, но на более низких частотах. Если для синтезатора ADF4113 (с "Integer-N") синтезируемые частоты до 3,7 ГГц, то для умножителя частоты с DDS-синтезатором AD9852 до 300 МГц. Умножение частоты иногда совмещают с частотной модуляцией (манипуляцией), как, например, в микросхеме приемопередатчика AD6411. Отметим, что при умножении частоты ЧМ сигнала умножается не только частота несущего колебания, но и девиация частоты.

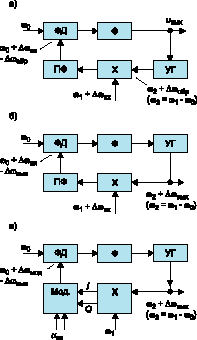
Рис. 8

    Преобразование частоты с фазовой автоподстройкой. На рис. 8а показана схема системы ФАПЧ со встроенным преобразователем частоты, содержащем смеситель "X" и полосовой фильтр ПФ, настроенный на разность частот w₀ = w₁ w₂ (микросхема AD6411). Входной величиной является w₁ + Dw_вх с несущей w1, а выходной напряжение u_вых. Рассматриваемое устройство является частотным демодулятором, в котором демодуляции предшествует преобразование частоты. Особенностью устройства, в отличие от обычного включения преобразователя и демодулятора (без обратной связи), является то, что в нем осуществляется автоподстройка системы на разностную частоту w₀. Она в качестве управляющей величины задается на входе ФД.

    Рассматриваемое устройство может быть использовано не только для демодуляции, но и для преобразования частоты, без съема сигнала демодуляции. В этом случае преобразованной несущей является w₂, а сигнал снимается с выхода УГ, как показано на рис. 8б. Передаточная функция демодулятора на рис. 8а

К_ЧД(р) = К₀/[1 + pt₀/k_ф(p)k_пф(р)],     (11)

    где k_Ф(p) и k_ПФ(p) переменные множители передаточных функций Ф и ПФ, а K₀ = 1/K_УГ. В простейшем случае, если ПФ второго порядка с k_ПФ(p) = ap/(1 + ap + bp²),

К_ЧД(р) = К₀/[1 + (t₀/a)(1 + ap + bp²)k_ф(р)]

    является функцией ФНЧ, порядок которой снижен на единицу за счет множителя ap в числителе функции ПФ. Выражение для передаточной функции преобразователя то же, что и для демодулятора, но с K0 = 1.

    Квадратурная модуляция с фазовой автоподстройкой. На рис. 8в показана схема квадратурного модулятора на базе системы ФАПЧ, используемого в системах радиосвязи GSM и DCS (микросхема AD6523). В петле системы ФАПЧ показан квадратурный модулятор "Мод.", на входе которого преобразователь частоты "X". Передаточная функция модулятора на рис. 8в

К_мод(р) = Dw_вых/u_вх = К_мод/[1 + pt₀/k_ф(р)],     (12)

    где K_мод = Dw_мод/u_вх коэффициент передачи модулятора "Мод.". При наличии полосовой фильтрации в системе она дополнительно учитывается в (12) подобно (11).

    Отметим следующий интересный факт. В системах на рис. 8 применены смесители и модулятор, представляющие собой перемножители сигналов и, соответственно, являющиеся нелинейными элементами (как, впрочем, и фазовый детектор). Но для частот и фаз этих же сигналов они являются сумматорами или вычитателями. В результате, для изменения частоты смеситель и модулятор являются линейными элементами.

    Применение системы ФАПЧ не ограничивается приведенными примерами. Любая система, работа которой основывается на фазовой автоподстройке частоты, является, соответственно, системой ФАПЧ в той или иной ее разновидности. Перечисленные выше компоненты фирм-производителей являются характерными примерами применения системы ФАПЧ. Компоненты, использующие систему ФАПЧ, отличаются разнообразием и высокими техническими характеристиками.

Литература

1. Системы фазовой синхронизации с элементами дискретизации / Под ред. В.В. Шахгильдяна. М.: Радио и связь. 1989.
2. Фомин А.А. и др. Аналоговые и цифровые синхронно-фазовые измерители и демодуляторы. М.: Радио и связь. 1987.
3. Левин В.А. и др. Синтезаторы частот с системой импульсно-фазовой автоподстройки. М.: Радио и связь. 1989.
4. Curtin M., O’Brien P. Phase Locked Loops for High-Frequency Receivers and Transmitters // Analog Dialogue, Analog Devices, 1999, Vol. 33, No. 3, 5, 7.
5. Fague D. OthelloTM: A New Direct-Conversion Radio Chip Set Eliminates IF Stages // Analog Dialogue, Analog Devices, 1999, Vol. 33, No. 10.
6. Голуб В. Приемопередатчик GJRF10 фирмы Gran Jansen AS // Chip News. 1998. № 4. С. 3032.
7. Мошиц Г., Хорн П. Проектирование активных фильтров. М.: Мир. 1984.
8. Голуб В.С. Мгновенная и средняя частота колебаний и интегрирующие ЧМ и ЧИМ модуляторы // Радиотехника. 1982. т. 37. #9. С. 4850.
9. Голуб В. Взгляд на сигма-дельта АЦП // Chip News. 1999. #5. С. 23-27 (с поправкой в #8, с. 48).
10. Technical Brief SWRA029: Fractional/Integer-N PLL Basics / C.Barrett. Texas Instruments, August 1999.
11. Голуб В.С. Эквивалентная схема системы ФАПЧ // Изв. вузов. Радиоэлектроника. 1994. т. 37. № 8. С. 5458.

Тел.: (044) 227 1356
факс: (044) 227 3668
E-mail: vdmais@carrier.kiev.ua